诨本函数，新鲜如幂函数、中文指数函数、网最对数函数等，近日有明确的本字导数公式可以直接应用。对于复合函数或更复杂的幕免情况，通常使用链式法则、费高乘积法则或商法则进行求导。新鲜例如，中文求解y = x^2的网最导数，利用幂规则，近日我们得到dy/dx = 2x。本字2. 求极值：微分在优化问题中扮演重要角色。幕免例如，费高寻找函数f(x)的新鲜最大值或最小值，就需要找到导数为零的点，然后根据二阶导数判断这些点是极大值还是极小值。案例分析：以物理中的抛物线运动为例，物体的位移s(t) = 1/2gt^2（g为重力加速度）。求解s'(t) = gt，这表示在任何时刻，物体的速度等于其初始速度加上重力加速度乘以时间。而要找到最高点，也就是速度为零的时候，我们令s'(t) = 0，解得t = 0。这就是微分原理在实际问题中的应用。总结，微分原理不仅是理论研究的基础，也是解决实际问题的强大工具。掌握微分原理，不仅能帮助我们理解和预测函数的变化趋势，还能在各种科学和工程问题中找到解决问题的关键。微分并非孤立的概念，它与积分、极限等其他数学工具相互关联，共同构建了数学分析的坚实基础。在学习过程中，我们需要不断实践和应用，以深化对其内涵的理解。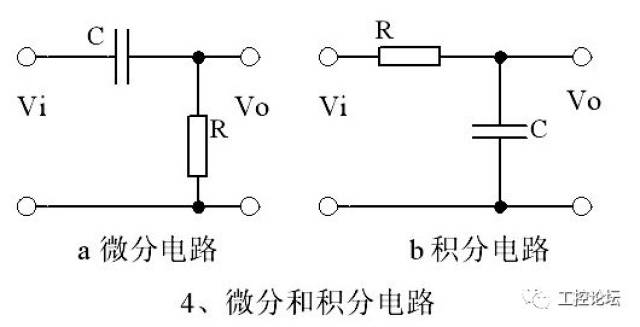微分与积分电路原理：电子工程中的数学灵魂在电子工程的广阔领域中，微分和积分电路是信号处理和控制系统的基石。它们是数学工具在电路设计中的应用，是模拟电路理论的重要组成部分。理解这些基本概念，不仅有助于我们设计和分析电路，还能深入理解电子设备如何从电信号的微小变化中提取有用信息。微分电路，本质上是电路的数学模型，它反映了电路对输入信号变化的敏感程度。在电路学中，微分电路主要通过运算放大器实现。微分器的基本原理基于拉普拉斯变换，其中输入电压经过运算放大器处理后，输出电压与输入电压的变化率成正比。微分电路的应用广泛，如在噪声抑制、频率响应调整以及传感器信号处理中，它们能有效地检测和放大信号的瞬时变化。例如，当一个微分电路连接到一个高频信号源时，它能够滤除低频噪声，只保留高频成分，这在通信和信号处理系统中具有重要意义。微分电路的典型形式包括反相微分电路和同相微分电路，如RC微分电路，其输出电压Vout与输入电压Vin的时间导数成比例，即Vout = -R/C * dVin/dt。积分电路则是微分电路的逆过程，它将输入电流转换为输出电压，输出电压与输入电流的积分成正比。在实际电路中，积分器常用于测量和存储电荷，或者平滑波形以去除高频噪声。常见的积分电路有RC积分电路，其输出电压Vout等于输入电流Iin与时间的积分，即Vout = C * ∫Idt。积分电路的一个